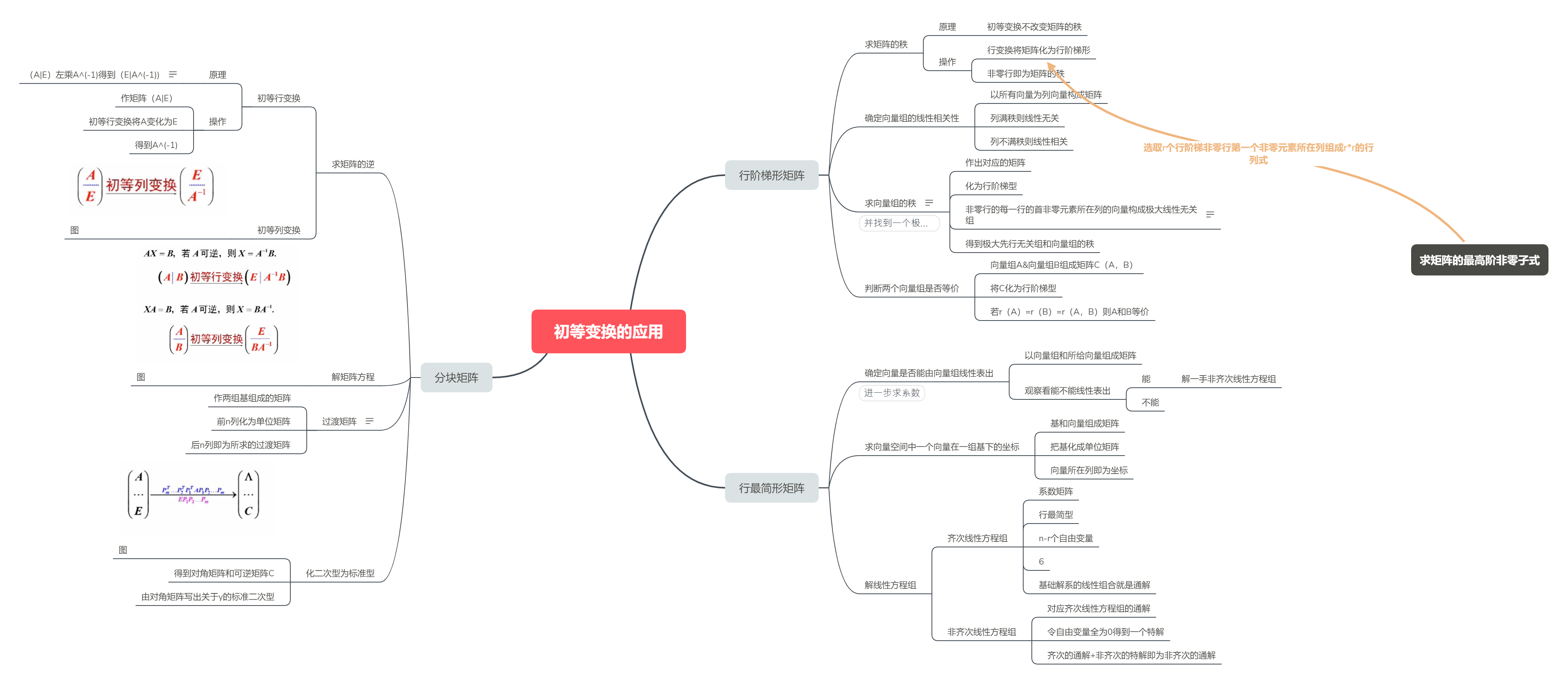
初等变换的应用
行阶梯形矩阵
求矩阵的秩
原理
- 初等变换不改变矩阵的秩
操作
- 行变换将矩阵化为行阶梯形
- 非零行即为矩阵的秩
确定向量组的线性相关性
- 以所有向量为列向量构成矩阵
- 列满秩则线性无关
- 列不满秩则线性相关
求向量组的秩
极大线性无关组所含向量个数为向量组的秩
作出对应的矩阵
化为行阶梯型
非零行的每一行的首非零元素所在列的向量构成极大线性无关组
极大先行无关组并不唯一
取每一行第一个首非零元素所在列的向量构成的极大先行无关组可能是若干个极大先行无关组的一个
秩即为极大先行无关组中向量的个数得到极大先行无关组和向量组的秩
判断两个向量组是否等价
- 向量组A&向量组B组成矩阵C(A,B)
- 将C化为行阶梯型
- 若r(A)=r(B)=r(A,B)则A和B等价
行最简形矩阵
确定向量是否能由向量组线性表出
以向量组和所给向量组成矩阵
观察看能不能线性表出
能
- 解一手非齐次线性方程组
不能
求向量空间中一个向量在一组基下的坐标
- 基和向量组成矩阵
- 把基化成单位矩阵
- 向量所在列即为坐标
解线性方程组
齐次线性方程组
- 系数矩阵
- 行最简型
- n-r个自由变量
- 6
- 基础解系的线性组合就是通解
非齐次线性方程组
- 对应齐次线性方程组的通解
- 令自由变量全为0得到一个特解
- 齐次的通解+非齐次的特解即为非齐次的通解
分块矩阵
求矩阵的逆
初等行变换
原理
(A|E)左乘A^(-1)得到(E|A^(-1))
左乘可逆矩阵相当于做初等行变换
操作
- 作矩阵(A|E)
- 初等行变换将A变化为E
- 得到A^(-1)
初等列变换
- 图
解矩阵方程
- 图
过渡矩阵
两组基之间的过渡矩阵
若X是在A基下的坐标,而Y是在B基下的坐标,则X,Y满足X=PY;过渡矩阵P为可逆矩阵。
- 作两组基组成的矩阵
- 前n列化为单位矩阵
- 后n列即为所求的过渡矩阵
化二次型为标准型
- 图
- 得到对角矩阵和可逆矩阵C
- 由对角矩阵写出关于y的标准二次型

