Ming
0%

LeetCode-64

Posted on Edited on In

LeetCode-64 最小路径和

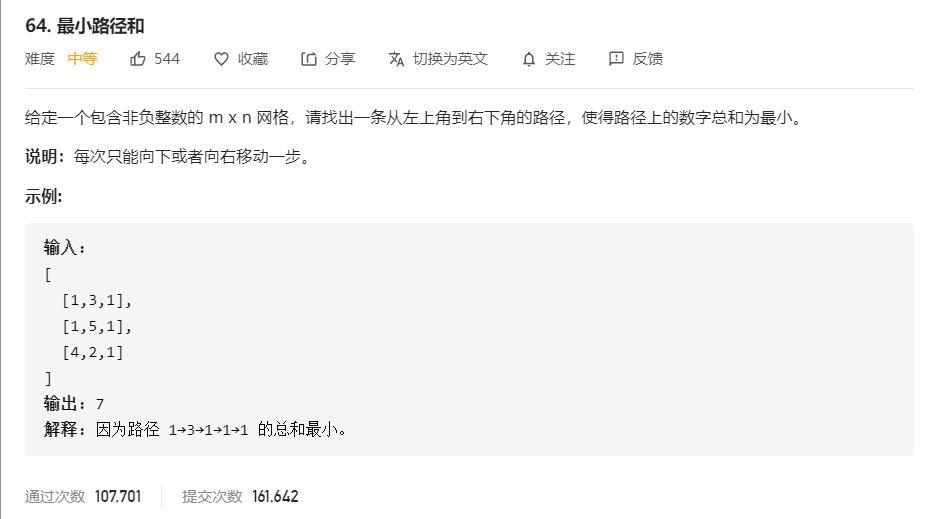
题目

结果

代码

主要思路是，每一个位置只能由上面或者左面的位置到达，从而有了dp的可能性。

标准版DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int minPathSum(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[][] dp = new int[row][col];
        dp[0][0] = grid[0][0];
        // Fill in the first row
        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        // Fill in the first column
        for (int i = 1; i < col; i++) {
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        }
        // Fill in the dp by rows
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }
}

空间优化版DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int minPathSum(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[] dp = new int[col];
        dp[0] = grid[0][0];
        
        for (int i = 0; i < row; i++) {
            // initial the dp[0]
            if (i != 0) {
                dp[0] = dp[0] + grid[i][0];
            }
            for (int j = 1; j < col; j++) {
                // If this is 1st row
                if (i == 0) {
                    dp[j] = dp[j - 1] + grid[i][j];
                } else {
                    dp[j] = Math.min(dp[j - 1], dp[j]) + grid[i][j];
                }
            }
        }
        return dp[col - 1];
    }
}

复杂度

  • 时间复杂度：O（m×n）

  • 空间复杂度：标准版O（m×n），优化版O（n）