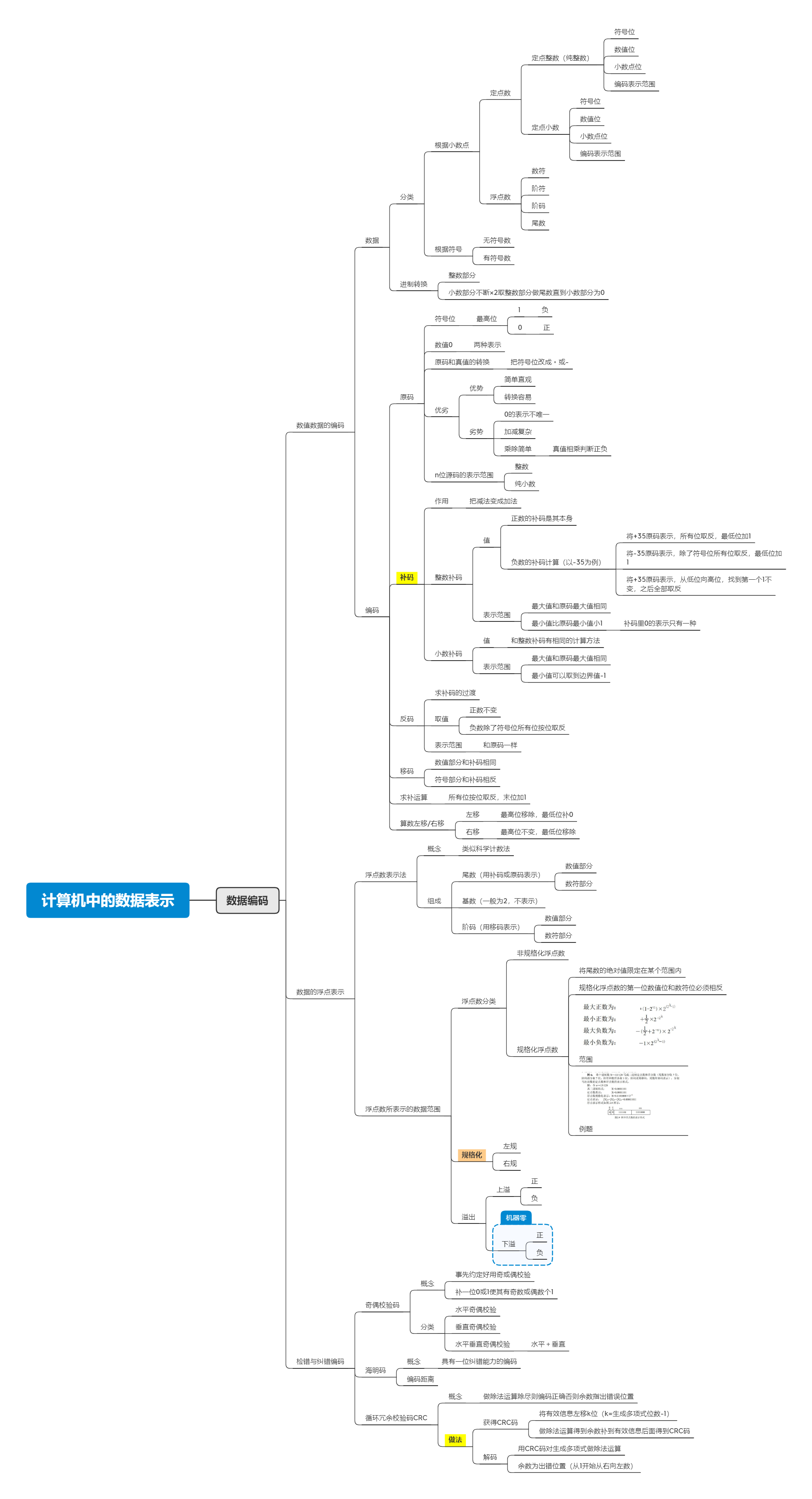
数据编码
数值数据的编码
数据
分类
根据小数点
定点数
定点整数(纯整数)
- 符号位
- 数值位
- 小数点位
- 编码表示范围
定点小数
- 符号位
- 数值位
- 小数点位
- 编码表示范围
浮点数
- 数符
- 阶符
- 阶码
- 尾数
根据符号
- 无符号数
- 有符号数
进制转换
- 整数部分
- 小数部分不断×2取整数部分做尾数直到小数部分为0
编码
原码
符号位
最高位
1
- 负
0
- 正
数值0
- 两种表示
原码和真值的转换
- 把符号位改成﹢或-
优劣
优势
- 简单直观
- 转换容易
劣势
0的表示不唯一
加减复杂
乘除简单
- 真值相乘判断正负
n位源码的表示范围
- 整数
- 纯小数
补码
作用
- 把减法变成加法
整数补码
值
正数的补码是其本身
负数的补码计算(以-35为例)
- 将+35原码表示,所有位取反,最低位加1
- 将-35原码表示,除了符号位所有位取反,最低位加1
- 将+35原码表示,从低位向高位,找到第一个1不变,之后全部取反
表示范围
最大值和原码最大值相同
最小值比原码最小值小1
- 补码里0的表示只有一种
小数补码
值
- 和整数补码有相同的计算方法
表示范围
- 最大值和原码最大值相同
- 最小值可以取到边界值-1
反码
求补码的过渡
取值
- 正数不变
- 负数除了符号位所有位按位取反
表示范围
- 和原码一样
移码
- 数值部分和补码相同
- 符号部分和补码相反
求补运算
- 所有位按位取反,末位加1
算数左移/右移
左移
- 最高位移除,最低位补0
右移
- 最高位不变,最低位移除
数据的浮点表示
浮点数表示法
概念
- 类似科学计数法
组成
尾数(用补码或原码表示)
- 数值部分
- 数符部分
基数(一般为2,不表示)
阶码(用移码表示)
- 数值部分
- 数符部分
浮点数所表示的数据范围
浮点数分类
非规格化浮点数
规格化浮点数
- 将尾数的绝对值限定在某个范围内
- 规格化浮点数的第一位数值位和数符位必须相反
- 范围
- 例题
规格化
- 左规
- 右规
溢出
上溢
- 正
- 负
下溢
- 正
- 负
检错与纠错编码
奇偶校验码
概念
- 事先约定好用奇或偶校验
- 补一位0或1使其有奇数或偶数个1
分类
水平奇偶校验
垂直奇偶校验
水平垂直奇偶校验
- 水平+垂直
海明码
概念
- 具有一位纠错能力的编码
编码距离
循环冗余校验码CRC
概念
- 做除法运算除尽则编码正确否则余数指出错误位置
做法
获得CRC码
- 将有效信息左移k位(k=生成多项式位数-1)
- 做除法运算得到余数补到有效信息后面得到CRC码
解码
- 用CRC码对生成多项式做除法运算
- 余数为出错位置(从1开始从右向左数)