Ming
0%

Shortest Path

Posted on Edited on In

最短路径问题

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。算法具体的形式包括：

  • 确定起点的最短路径问题 - 也叫单源最短路问题，即已知起始结点，求最短路径的问题。在边权非负时适合使用Dijkstra算法，若边权为负时则适合使用Bellman-ford算法或者SPFA算法。
  • 确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
  • 确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
  • 全局最短路径问题 - 也叫多源最短路问题，求图中所有的最短路径。适合使用Floyd-Warshall算法。

用于解决最短路径问题的算法被称做“最短路径算法”，有时被简称作“路径算法”。最常用的路径算法有：

迪杰斯特拉

迪杰斯特拉 | Ming (m1ng.xyz)

Bellman Ford

求解单源最短路径问题的一种算法，由理查德·贝尔曼（Richard Bellman） 和 莱斯特·福特（英语：Lester Ford） 创立的。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行|V|-1次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高。

为什么要松弛|V|-1次？简单来说，含有V个节点的图中，两个节点间最多有v-1条边。松弛|V|-1次能确保最短路径被发现。

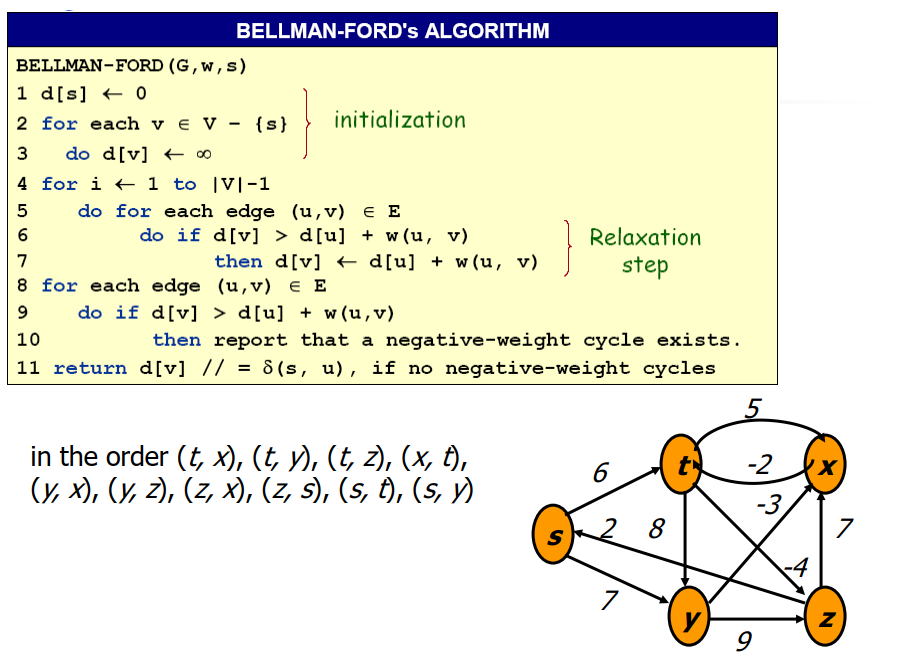
栗子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
package main

import (
	"fmt"
	"math"
)

func main() {
	var edges []Edge
	edges = append(edges, Edge{'A', 'B', -1}, Edge{'A', 'C', 3}, Edge{'B', 'C', 3}, Edge{'B', 'D', 2}, Edge{'B', 'E', 2}, Edge{'D', 'B', 1}, Edge{'D', 'C', 5}, Edge{'E', 'D', -3})
	BellmanFord(edges, 5, 'A')
}

const INFINITY = math.MaxInt32

type Edge struct {
	src   rune
	dest  rune
	wight int
}

func BellmanFord(graph []Edge, n int, src rune) {
	// nodes set
	nodes := make(map[rune]bool)
	for _, edge := range graph {
		if _, ok := nodes[edge.src]; !ok {
			nodes[edge.src] = true
		}
		if _, ok := nodes[edge.dest]; !ok {
			nodes[edge.dest] = true
		}
	}

	// distance from src to another node
	d := make(map[rune]int)
	for node := range nodes {
		d[node] = INFINITY
	}
	d[src] = 0

	// relaxation |v| - 1 times
	for i := 0; i < n-1; i++ {
		for _, edge := range graph {
			if d[edge.dest] > edge.wight+d[edge.src] {
				d[edge.dest] = edge.wight + d[edge.src]
			}
		}
	}

	for node, dist := range d {
		fmt.Printf("%c-->%c:%d\n", src, node, dist)
	}
}

Floyd Warshall

Floyd-Warshall算法（英语：Floyd-Warshall algorithm），中文亦称弗洛伊德算法或佛洛依德算法，是解决任意两点间的最短路径的一种算法[2]，可以正确处理有向图或负权（但不可存在负权回路）的最短路径问题，同时也被用于计算有向图的传递闭包。

Floyd-Warshall算法的时间复杂度为O(N^3)[4]，空间复杂度为O(N^2)。

松弛操作让我想起矩阵链乘：矩阵链乘积 | Ming (m1ng.xyz)

栗子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
package main

import (
	"fmt"
	"math"
)

func main() {
	var edges []Edge
	edges = append(edges, Edge{'A', 'B', -1}, Edge{'A', 'C', 3}, Edge{'B', 'C', 3}, Edge{'B', 'D', 2}, Edge{'B', 'E', 2}, Edge{'D', 'B', 1}, Edge{'D', 'C', 5}, Edge{'E', 'D', -3})
	FloydWarshall(edges, 5, 'A')
}

const INFINITY = math.MaxInt32

type Edge struct {
	src   rune
	dest  rune
	wight int
}

func FloydWarshall(graph []Edge, n int, src rune) {
	// C(k)[i][j] means weight of a shortest path from i to j with intermediate vertices belonging to the set {0,1,2,…,k}
	C := make([][]int, n)
	for i := range C {
		C[i] = make([]int, n)
	}

	// initialization
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			if i != j {
				C[i][j] = INFINITY
			}
		}
	}

	// conversion between letter and number
	for _, edge := range graph {
		C[edge.src-'A'][edge.dest-'A'] = edge.wight
	}

	for k := 0; k < n; k++ {
		for i := 0; i < n; i++ {
			for j := 0; j < n; j++ {
				// relaxation
				if C[i][j] > C[i][k]+C[k][j] {
					C[i][j] = C[i][k] + C[k][j]
				}
			}
		}
	}

	// output
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			if i != j {
				if C[i][j] > INFINITY/2 {
					fmt.Printf("%c-->%c:∞\n", i+'A', j+'A')
				} else {
					fmt.Printf("%c-->%c:%d\n", i+'A', j+'A', C[i][j])
				}
			}
		}
	}
}