Ming

缓存文件置换机制是电脑处理缓存存储器的一种机制。

电脑存储器空间的大小固定，无法容纳服务器上所有的文件，所以当有新的文件要被置换入缓存时，必须根据一定的原则来取代掉适当的文件。此原则即所谓缓存文件置换机制。

缓存文件置换方法有：

• 先进先出算法（FIFO）：最先进入的内容作为替换对象
• 最近最少使用算法（LFU）：最近最少使用的内容作为替换对象
• 最久未使用算法（LRU）：最久没有访问的内容作为替换对象
• 非最近使用算法（NMRU）：在最近没有使用的内容中随机选择一个作为替换对象

去年在搬瓦工买了一年的洛杉矶的VPS，用v2ray，注册了一个域名，开始很谨慎，用websocket伪装，用了几天，速度实在是慢。

于是我从websocket换成了KPS协议，速度快的飞起，youtube 1080P毫无压力，A few moments later。。。。。

被墙了。

数据结构、离散数学、计算机网络、算法，这些课都讲过这个算法，再加上我大一的时候看的《图解算法》，对迪杰斯特拉已经很熟悉了。

戴克斯特拉算法（英语：Dijkstra’s algorithm），又译迪杰斯特拉算法，亦可不音译而称为Dijkstra算法[6]，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法，并于3年后在期刊上发表[7][8][9]。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图[9]的单源最短路径问题[10][1][2]。

题目

743. 网络延迟时间

题目

1143. 最长公共子序列

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是：子序列不需要在原序列中占用连续的位置 。最长公共子序列问题是一个经典的计算机科学问题，也是数据比较程序，比如Diff工具，和生物信息学应用的基础。它也被广泛地应用在版本控制，比如Git用来调和文件之间的改变。

矩阵链乘积（英语：Matrix chain multiplication，或Matrix Chain Ordering Problem，MCOP）是可用动态规划解决的最佳化问题。给定一序列矩阵，期望求出相乘这些矩阵的最有效方法。此问题并不是真的去执行其乘法，而只是决定执行乘法的顺序而已。

因为矩阵乘法具有结合律，所有其运算顺序有很多种选择。换句话说，不论如何括号其乘积，最后结果都会是一样的。例如，若有四个矩阵ABCD，将可以有：

ABCD=(AB)(CD)=A(BCD)=A(BC)D=…

但括号其乘积的顺序是会影响到需计算乘积所需简单算术运算的数目，即其效率。例如，设A为一10 X 30矩阵，B为30 X 5矩阵与C为5 X 60矩阵，则：

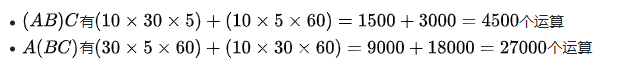
明显地，第一种方式要有效多了。既然已确认过此问题了，那要如何决定n个矩阵相乘的最佳顺序呢？可以比较每一顺序的运算量（使用蛮力），但这将需要时间O(2n)，是一种非常慢且对大n不实在的方法。那解决方法，如我们将看到的，是将问题分成一套相关的子问题。以解答子问题一次而再使用其解答数次，即可以彻底地得出其所需时间。此一方法称为动态规划。

N个矩阵（A1，A2，A3，，，An）链乘的最佳顺序，对于这个问题，它的子问题是什么？如何将它拆分成更小的子问题呢？

可以将这N个矩阵分成两部分，第一部分的最佳顺序是一个子问题，第二部分的最佳顺序也是一个子问题。那这两个子问题和大问题又如何建立联系呢？

将N个矩阵分成两部分，有多种不同的划分方法，三个矩阵链乘有2种划分方法：（AB）C和A（BC）

我们去尝试所有的划分方法，求得每种划分方法需要的计算数，取最小的作为N个矩阵链乘的最优解。

划分而得的两部分又可以拆分成更小的子问题，这时候动态规划就能发挥威力，我们自下而上去求解，将求得的结果存在一张表中，方便复用。

由此可见，动态规划问题的主要求解思路就是如何寻找最优解问题的子问题，以及如何将大问题和子问题联系起来。